Algorithm Notes: Binary Heap

Definition

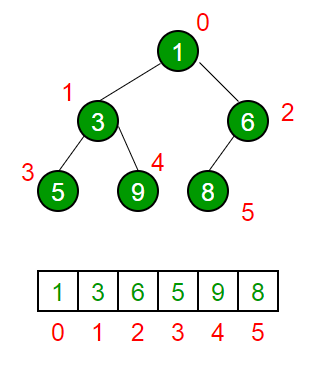
A Binary Heap is a complete Binary Tree. It is either a Min Heap, where parent node's value is less than or equal to its children's, or a Max Heap, where parent node's value is greater than or equal to it's children's.

It is represented as an array, where

the root node is at Arr[0];
for the $i^{th}$ node Arr[i],
- Arr[(i-1)/2] returns its parent node;
- Arr[2*i+1] returns its left child node;
- Arr[2*i+2] returns its right child node;

Operation

Construction

The fundamental idea of binary heap construction is that, ==starting from the last parent node util the root node, construct a heap for each with all its children, because each branch node and its children compose a heap==.

Given the struct of the heap:

class BinaryHeap {
    int[] heap;
  int heapSize;        //current number of elements in heap
  int capacity;        //maximum size of the heap
}

Conventionally, heap[0] will work as the storage for temporary data, so the real heap data will start from heap[1] to heap[heapSize].

void Construct() {    
  for (int i = heapSize/2; i > 0; i--) {
    Heapify(i);
  }
}

void Heapify(int start) {
  heap[0] = heap[start];
  int son = start*2;
  while (son <= heapSize) {
    if (son < heapSize && heap[son] < heap[son+1])
      son++;
    if (heap[0] >= heap[son])
      break;
    heap[son/2] = heap[son];
    son *=2;
  }
  heap[son/2] = heap[0];
}

As we see, we extract a method called Heapify, which is a core function in binary heap. It is used for maintaining the property of the subtree with given root.

The following illustrates an example of the process:

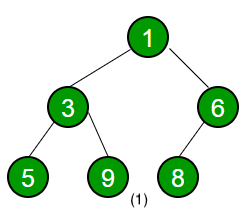
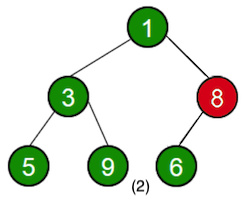
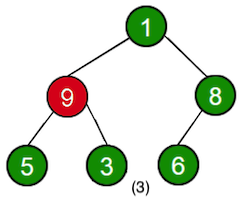
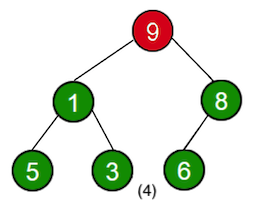
The time complexity is $O(n)$ .

Insert

To insert an element into the heap, put the element at the end and then traverse up to fix the heap property, just like the construction process. The time complexity is $O(logn)$ .

bool Insert(int x) {
    if (heapSize == capacity)
    return false;
  int i = ++heapSize;
  while (i > 0 && x > heap[i/2]) {
    heap[i] = heap[i/2];
    i/=2;
  }
  heap[i] = x;
  return true;
}

Delete

After removing the top element from the heap, place the last element at top, then fix the heap property. The time complexity is $O(logn)$ .

int Delete() {
  if (heapSize == 0) 
    return false;

  int x = heap[1];
  heapSize--;
  Heapify(1);
  return x;
}

Application

Heap Sort

Using binary heap to sort an array takes $O(nlogn)$ time. The idea is that extract the top element of the heap and put it at the end of the heap array, then fix the heap property.

while(heapSize > 0) {
  int temp = heap[heapSize];
  heap[heapSize] = heap[1];
  heap[1] = temp;
  heapSize--;
  Heapify(1);
}

Priority Queue

Binary Heap gives a maximum efficient implementation of priority queue. It provides the basic operation like insert, extract, peek priority value. Besides, it can do other more complicated operations, e.g. insert and extract a bunch of priority values(leetcode), change priority, merge multiple priority queues(leetcode).

Magicbell's Website